Baekjoon) 1916 최소비용 구하기 - Python , 다익스트라 알고리즘

💡 나의 접근 방법

---

문제를 읽고 다익스트라, 플로이드 와샬 알고리즘으로 푸는 문제임을 알았다.

시간 제한이 0.5 초 이므로 다익스트라 알고리즘으로 풀기로 했다.

💡 결과

---

# 1916 최소 비용구하기 G5
import heapq
import sys
input = sys.stdin.readline
N = int(input())
M = int(input())
INF = 1e8
graph = [[] for _ in range(N+1)]
distance = [INF] * (N+1)
for i in range(M):
    a,b,c = map(int,input().split())
    graph[a].append((b,c))
start,end = map(int,input().split())


def dijkstra(start):
    q = []
    heapq.heappush(q,(0,start)) # 힙큐는 첫번째 인덱스를 오름차순하기 때문에 거리가 앞에 와야함
    distance[start] = 0
    while q:
        dis, node = heapq.heappop(q)
        for next in graph[node]:
            cost = next[1] + dis
            if distance[next[0]] > cost:
                distance[next[0]] = cost
                heapq.heappush(q,(cost,next[0]))

dijkstra(start)
print(distance[end])

다익스트라 알고리즘을 생각하면서 문제를 풀었으나 시간초과 에러가 발생했다.

이유는 이미 방문했노드를 처리해주지 않아서 이다.

if distance[node] < dis: # 중복을 피하기 위한 조건 : 이미 더 짧은 경로로 방문한 적이 있음
            continue

while문 힙에서 나온 dis, node 는 이미 방문했던 distance[node] 값보다 클 수 있다. 따라서 이 경우를 처리 해준다.

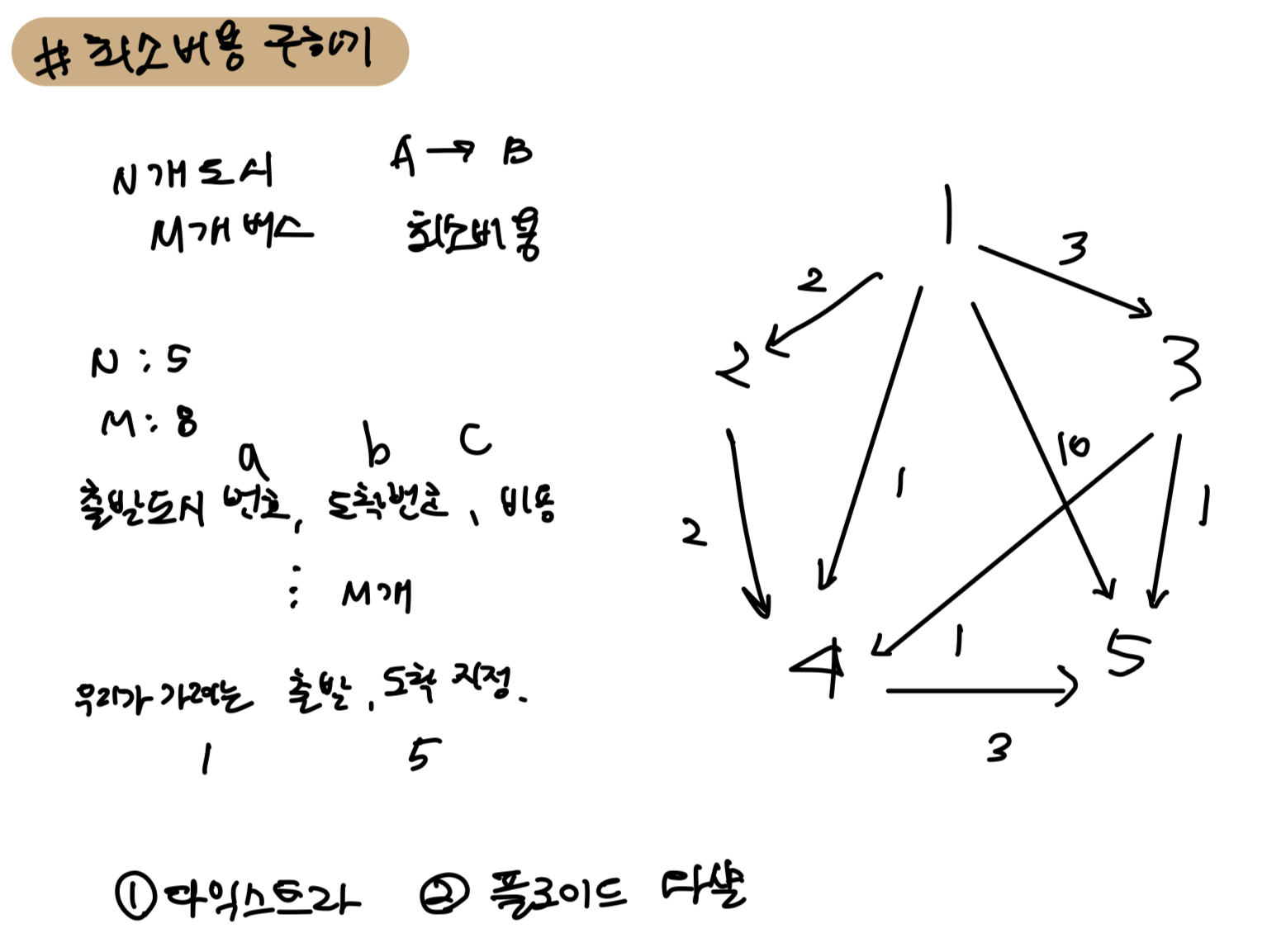
그림에서 예를 들면 1->5 10/ 은 이미 4로 설정되었었기 때문에 10을 처리해주는 것을 continue 해주는 것이다.

 

📖 정답 코드

# 1916 최소 비용구하기 G5
import heapq
import sys
input = sys.stdin.readline
N = int(input())
M = int(input())
INF = 1e8
graph = [[] for _ in range(N+1)]
distance = [INF] * (N+1)
for i in range(M):
    a,b,c = map(int,input().split())
    graph[a].append((b,c))
start,end = map(int,input().split())


def dijkstra(start):
    q = []
    heapq.heappush(q,(0,start)) # 힙큐는 첫번째 인덱스를 오름차순하기 때문에 거리가 앞에 와야함
    distance[start] = 0
    while q:
        dis, node = heapq.heappop(q)

        if distance[node] < dis: # 중복을 피하기 위한 조건 : 이미 더 짧은 경로로 방문한 적이 있음
            continue

        for next in graph[node]:
            cost = next[1] + dis
            if distance[next[0]] > cost:
                distance[next[0]] = cost
                heapq.heappush(q,(cost,next[0]))

dijkstra(start)
print(distance[end])

 

💡느낀 점

---

최단 경로문제는 왠만하면 다익스트라로 접근 한 것같다.

코드 참고 없이 다익스트라를 구현해서 결과가 잘 나오니까 뿌듯했는데! 시간초과가 너무 아쉬웠다..

이번기회에 놓친 조건문을 잡을 수 있었고, 다익스트라 알고리즘에 자신이 생긴것 같다!!

 

 

1916번: 최소비용 구하기